Cause of an electric fire(Is only the leak a cause?)

Information like "It seems that the cause of this fire depends on the leak" is asked well by reporting the newspaper and the television. Causes other than the leak have been hardly heard by reporting an electric fire. Does a fire happen really so much because of the leak?

I think that there are few households where the leak breaker (earth leakage breaker) has not adhered now. I do not think that the fire caused by a short circuit happens easily if the leak breaker has adhered.

I think that generation of heat of connected part of the outlet and the electric wire (Joule heat and arc heat), a tracking phenomena, and various shorts (short-circuit) are the major causes of the cause of an electric fire. I think very little caused by the leak.

If the leak is not understood well, I think hope without saying the leak and the leak.

What is the leak?

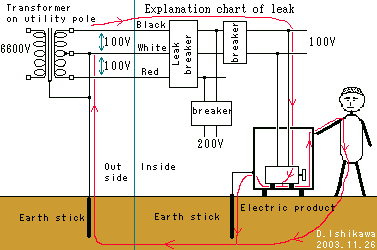Leak explanation chartAn interior wiring and electromechanical apparatus are covered with the insulation thing so that electricity should not leak from the part where original flows.

Electricity leaks from the part where the electricity of wiring and an electric product flows when this insulation thing is deteriorated or tears and it flows to the earth finally as shown in left figure. This current returns from the earth of the transformer (It is called a transformer on the pillar) on the utility pole (earth) to the transformer on the pillar. How of such electricity for the leakage is called a leak. This current is called the current leakage or Cara currents in the matrix.

It explains details around here in detail on the page of Electric shock and earth.

It is thought that it is all said to leak from the part where electricity flows originally with the leak in a wide meaning. It can be said that the tracking and the short circuit of the electric wire are leaks when being think in the future. It is a leak that the insulation of capacitors of parts tears, it is short-circuited, and an electric product breaks down.

I think that it should indicate Cara currents in the matrix by the leak because it is confused when these are all called a leak.

An electric fire because of generation of heat of connected part in electric circuit

Connect connected part of connected part of the outlet in the entrance and the wall and electric wires and electric wires by the low resistance originally the inset in.

The contact resistance grows when there is shortage in the outlet as the inserted plug is loose, and when the current flows, heat is generated. The copper wire rusts for a long time, speaks with a local accent, and when heat is generated, the contact resistance grows further. Then, heat is generated further because of Joule heat and the arc heat and it finally comes to ignite.

Outlet and plug that generates heat

This photograph cannot take electricity from the outlet by the outlet part's generating heat. The electric wire connection part of the plug generates heat. The part of the copper of the plug rusts and discolors, and the part of the electric wire scorches and has discolored. The outlet part scorches and externals crack. The plate part is relieved and transformed. Please exchange it at once for the new article if there is such a part.

The microwave oven was not already able to be sometimes used for a certain customer's house and it has visited years how many are to talk about the previous state. 100V has not come to the exposure outlet of the wall. Nothing has not fallen into the breaker. It was surprised to go up back of the ceiling. There was one-place light during darkness. It had wired for the electric wire by the amateur, and connected part was twisted. It sparked in the connected part. Even if a fire happens when, it is not mysterious.

Measures

An electric fire caused by generation of heat such as electric wires thin

The electric wire generates heat in using the cord bundled while rolled in the drum of making a thin vinyl cord the extension cord of the air conditioner and the insulation thing is transformed, and it is likely to be short (short-circuit) and to arrive at a fire.

Might heat be generated, and the electric wire of the trunk line ignite when it uses electricity too much when the breaking current of the current breaker of the trunk line when the current breaker (leak breaker) has not adhered to the trunk line though the drawing in electric wire and the trunk line in the house are thin is larger than the thickness of the electric wire.

Measures

An electric fire by tracking phenomenon

It often hears of the tracking phenomenon of the word recently. Might it wait, and the dust come to conduct electricity easily in the root of the plug that does to the outlet for a long time because of moisture rain, the be dewy, and in air dust this.

When the current flows, heat is generated. It accelerates gradually and dust finally carbonizes. Then, it becomes easy to conduct electricity further. The current finally increases with accelerating speed and it becomes an ignition.

Generation of heat when an electric product is used might promote the carbonization of dust if the loose connection between the plug and the outlet joins this, and, in addition, the tracking phenomenon advances.

Measures

An electric fire by short of electric wire (short-circuit)

  Because the end is short (short-circuit) and an igniting translation in the above-mentioned tracking phenomenon, it can be thought the ignition on which this depends short, too. However, it is likely to ignite simply because of short circuit.

  When furniture etc. have gotten on on the electric wire of the table tap (extension cord), the cord might collapse for a long time, it transform, and the electric wire be short. Moreover, the coating of the cord might tear when a sharp part of the metal always comes in contact with the cord and it be short.

  The rat might be short as the electric wire is bitten in the back of the ceiling and the wall.

  It sets sparks flying between electric wires, it ignites to other one that burns easily, and it becomes a fire when the electric wire is short-circuited and it enters the state of slight.

Measures

An electric fire because of leak

  I do not think the fire caused by a short circuit for the so many examples to exist now. Because the leak breaker (earth leakage breaker) works when the leak happens (Operate by 15-30mA) and the power supply stops. It seems that it is rare though it is likely to be likely to ignite if the electric power of 100V30mA (power) is 3W, and this concentrates on one point.

  However, there is a possibility of becoming a fire if the leak happens between from lead-ins to the switchboard even if the leak breaker has adhered. The probability of the leak seems to be low putting in the electric wire tube of the cable because it has often wired for a part comprehensible in the house the distance short. it however

  When the leak breaker has not adhered in house of corresponding old, it is possible to become a fire by the leak. It is in a word because of the tear of insulation somewhere of the interior wiring, the leak such as the Ras nets of the wall, the flow of the current to the earth, and the return to the transformer on the pillar.

  At this time, it is likely to generate heat by the resistance of the Ras net and to become a fire.

Measures

An electric fire due to earthquake

  In the Hanshin-Awaji (Kobe) Earthquake on January 17, 1995, a fire thought that electricity was a cause of breaking out occupied about 1/4 of the all fires. The cause had something etc. that were short-circuited when damage receiving energized to wiring with the one and the falling furniture, etc. by generation of heat of the hot plate tool such as falling electric stoves and ignited.

Measures