LC reactance(calculation of LC reactance by each frequency)
It is troublesome to calculate the reactance ( impedance ) separately by each frequency when the capacitor and the coil are used. If an other value is understood, it is likely to be able to design easily. Next, I want to calculate these values beforehand.
What is reactance?
The coil (inductance L) and the capacitor (capacitance C) show resistance different from direct current in the exchange. The value that corresponds to this resistance is called reactance (The unit is Ω) in the exchange. This reactance reaches a value different depending on frequency (f) of the exchange.
Operation of CR series circuit(cutoff frequency of CR filter)
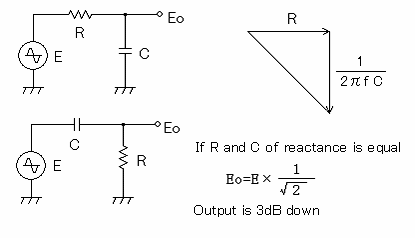 There
is a thing that the circuit like the following comes out frequently with the
capacitor and the coupling capacitor etc. of the CR filter in the electrical
circuit. There is hesitating in good when the value of the capacitor is made
which place at this time.
There
is a thing that the circuit like the following comes out frequently with the
capacitor and the coupling capacitor etc. of the CR filter in the electrical
circuit. There is hesitating in good when the value of the capacitor is made
which place at this time.
Generally, it is time when becoming a cutoff frequency is equal the impedance value of the capacitor and resistance. In this case, the output voltage decreases by 3dB.
I think that the value of the capacitor can often select this cutoff frequency to the standard, and the reactance table of the following capacitor becomes reference very much when the circuit is designed.
However, it is noted not to become it like this for the bypass capacitor of the emitter of a general amplifier.
Reactance calculation value of capacitor [Ω]
The reactance of capacitor C(impedance) in each frequency Zc is calculated by the following expression.
Zc = 1/(2πf C)
| 50Hz | 60Hz | 100Hz | 300Hz | 1kHz | 3kHz | 10kHz | 100kHz | 1MHz | 10MHz | 100MHz | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10pF | 318M | 265M | 159M | 53.1M | 15.9M | 5.31M | 1.59M | 159k | 15.9k | 1.59k | 159 |
| 100pF | 31.8M | 26.5M | 15.9M | 5.31M | 1.59M | 531k | 159k | 15.9k | 1.59k | 159 | 15.9 |
| 1000pF | 3.18M | 2.65M | 1.59M | 531k | 159k | 53.1k | 15.9k | 1.59k | 159 | 15.9 | 1.59 |
| 0.01μF | 318k | 265k | 159k | 53.1k | 15.9k | 5.31k | 1.59k | 159 | 15.9 | 1.59 | 159m |
| 0.1μF | 31.8k | 26.5k | 15.9k | 5.31k | 1.59k | 531 | 159 | 15.9 | 1.59 | 159m | 15.9m |
| 1μF | 3.18k | 2.65k | 1.59k | 531 | 159 | 53.1 | 15.9 | 1.59 | 159m | 15.9m | 1.59m |
| 10μF | 318 | 265 | 159 | 53.1 | 15.9 | 5.31 | 1.59 | 159m | 15.9m | 1.59m | 159μ |
| 100μF | 31.8 | 26.5 | 15.9 | 5.31 | 1.59 | 531m | 159m | 15.9m | 1.59m | 159μ | 15.9μ |
It guarantees whether these values are neither calculation values to the last nor to actually become this value.
Reactance calculation value of coil [Ω]
The reactance of coil L(impedance) in each frequency ZL is calculated by the following expression.
ZL = 2πf L
| 50Hz | 60Hz | 100Hz | 300Hz | 1kHz | 3kHz | 10kHz | 100kHz | 1MHz | 10MHz | 100MHz | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1μH | 314μ | 377μ | 628μ | 1.88m | 6.28m | 18.8m | 62.8m | 628m | 6.28 | 62.8 | 628 |
| 10μH | 3.14m | 3.77m | 6.28m | 18.8m | 62.8m | 188m | 628m | 6.28 | 62.8 | 628 | 6.28k |
| 100μH | 31.4m | 37.7m | 62.8m | 188m | 628m | 1.88 | 6.28 | 62.8 | 628 | 6.28k | 62.8k |
| 1mH | 314m | 377m | 628m | 1.88 | 6.28 | 18.8 | 62.8 | 628 | 6.28k | 62.8k | 628k |
| 10mH | 3.14 | 3.77 | 6.28 | 18.8 | 62.8 | 188 | 628 | 6.28k | 62.8k | 628k | 6.28M |
| 100mH | 31.4 | 37.7 | 62.8 | 188 | 628 | 1.88k | 6.28k | 62.8k | 628k | 6.28M | 62.8M |
| 1H | 314 | 377 | 628 | 1.88k | 6.28k | 18.8k | 62.8k | 628k | 6.28M | 62.8M | 628M |
It guarantees whether these values are neither calculation values to the last nor to actually become this value.